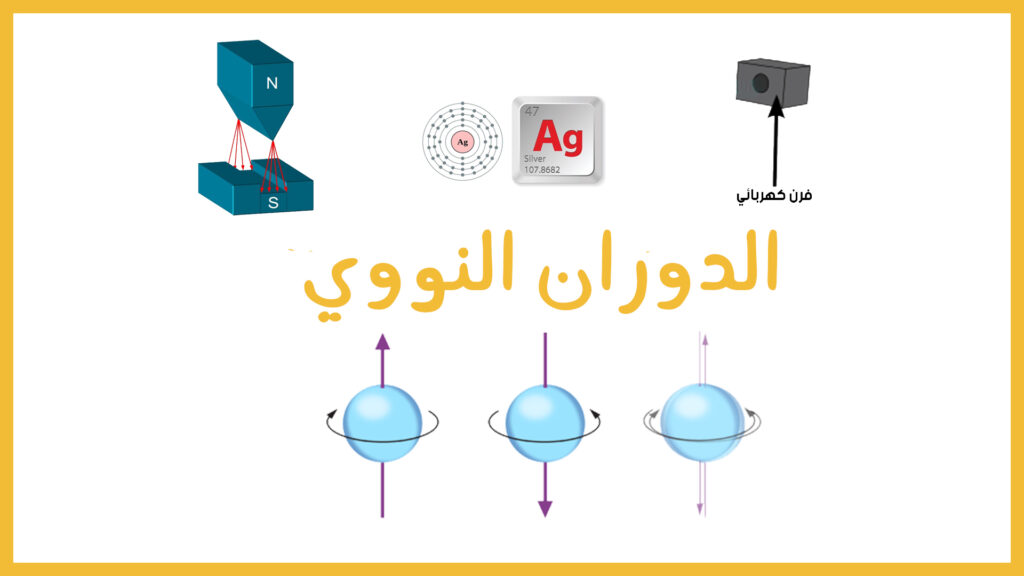
في ميكانيكا الكم لا تنطبق مفاهيمنا المعروفة في الفيزياء الكلاسيكية حيث لا يوجد اي معنى للقياسات الدقيقة هنا فالانظمة الكمية تحكمها قوانينها الخاصة التي اثبتت دقتها في التجارب المختلفة والتي وافقت نتائجها تنبؤات ميكانيكا الكم .
حيث تمثل ميكانيكا الكم مجموعة من النظريات الفيزيائية التي تفسر الظواهر على مستوى الجسيمات الذريّة و دون الذريّة والتي تتميز بالطبيعة المزدوجة (الجسيم -الموجة) . ميكانيكا الكم هي تعميم للفيزياء الكلاسيكية لإمكانية تطبيقها على المستويين الذري والعادي(و لكن لا يظهر تأثيرها على المستوى العادي).
-في الفيزياء الكلاسيكية، يمتلك الجسم الدّوار خاصية تعرف بإسم الزخم الزاوي. إن الزخم الزاوي هو شكل من أشكال القصور الذاتي، الذي يعكس: حجم الجسم وشكله وكتلته وسرعته الدورانية.
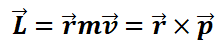
حيث تمثل الرموز :
(m):كتلة الجسم
(v):السرعة
(p): متجه الزخم الخطي (m*v)
(r): بعد متجة المسافة بين الجسم عن مركز الدوران
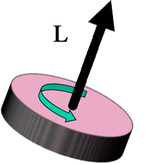
و تنطبق هذه المعادلة على الاجسام كلها بإختلاف حجمها و لكن في المستوى الذري لدوران الالكترون مثلا فإن قيم الزخم ستأخذ قيمًا منفصلة و غير مستمرة كما الحال في الاجسام الكبيرة .
يتم نقل المعادلة لميكانيكا الكم، عن طريق إعادة ترجمة r كمؤثر كمي للموضع وp كمؤثر كمي لكمية الحركة. وتصبح L مؤثر يدعى “مؤثر الزخم الزاوي المداري”.
و اي جسيم مشحون يملك اي نوع من الزخم سيملك مجال مغناطيسي و ايضا سيتأثر بأي مجال مغناطيسي اخر(مثل الالكترون المشحون بشحنة سالبة الموجودة في مجال مغناطيسي خارجي).
-تمتلك الجسيمات الذرية ودون الذرية خاصية تعرف باسم الزخم الزاوي الدوراني أو الدوران .
احدى التجارب التي اجريت لاثبات خاصية دوران الالكترون هي تجربة شتيرن غيرلاخ عام 1922 (Stern-Gerlach experiment)التي تكونت من حزمة من ذرات الفضة الموجهة خلال مجال مغناطيسي غير منتظم (مكون من قطب مدبب مما يزيد من شدة المجال عند المنشئ و قطب اخر مقعر بحيث تقل شده المجال عنده مما ينشئ مجال مغناطيسي غير متجانس )حيث ادى ذلك الى تجزئة الحزمة الى جزئين حيث لوحظ على شاشة الكاشف ان الالكترونات تنحرف اما لاعلى او لاسفل حسب اتجاه دورانها و انحرافها يؤكد على مغناطيسيتها الناتجة عن عزم الدوران.
-لم يكن العزم المغزلي للإلكترون معروفا وقتها(الناشئ عن دورانه حول نفسه). ولكن كان معروفا أن العزم المغناطيسي للذرة يتكون من محصلة العزم المداري لجميع الإلكترونات فيها، حيث يمكن اهمال العزم المغناطيسي الناشيء عن النواة الذرية . ولكن ذرة الفضة لها عزم مغناطيسي متمثل في الـ spin (الدوران)الذي يمتلكه الإلكترون الموجود في غلافها الاخير , لأن جميع الإلكترونات الأخرى في ذرة الفضة لها عزم مداري يساوي صفر طبقا لنموذج الأغلفة الإلكترونية الكاملة في الذرات.
الإلكترون 5s في ذرة الفضة – وهو الغلاف الخارجي – له عدد الكم المداري {l=0} (حيث ليس له عزما مداريا). فتكون محصلة العزم المداري لذرة الفضة مكونة من العزم المغزلي spin لهذا لإلكترون فقط، وتتصرف ذرة الفضة بأكملها كجسيم له عدد كمي مغزلي 1/2 . ولكن الفرق بين الإلكترون وذرة الفضة أن ذرة الفضة متعادلة كهربائيا أما الإلكترون فهو يحمل شحنة سالبة( 10-19*1.6كولوم) . وبناء على ذلك لن تتأثر ذرة الفضة بقوة لورينتز أثناء مرورها في المجال المغناطيسي . ويكون التأثير الحاصل هو تفاعل العزم المغناطيسي لذرة الفضة مع المجال المغناطيسي الخارجي الغير متجانس .
-تمتلك الإلكترونات والبروتونات والنيوترونات والنواة الكاملة حركة دورانية وغالبًا ما يتم تمثيلها ككرات دوران صغيرة(ورغم عدم دقة الوصف، فإن هذه ليست طريقة سيئة للتفكير في الدوران النووي ما لم نأخذ هذا المقياس بعيداً). لذلك يجب الاعتراف بالعديد من الاختلافات الرئيسية:
1) الجسيم لا يدور في الواقع.
2) الدوران (او البرم) (S)، مثل الكتلة، هو خاصية أساسية للطبيعة ولا ينشأ عن عمليات أساسية اخرى.
3) يتفاعل الدوران(S) مع المجالات الكهرومغناطيسية في حين يتفاعل الزخم الزاوي الكلاسيكي (L) مع مجالات الجاذبية.
4) يتم قياس قيم الدوران(S) كميًا ، مما يعني أنه لا يمكن أن يأخذ إلا مجموعة محدودة من القيم المنفصلة.
*الدوران (البرم)(S) صفة أصيلة للجسيم، لا ترتبط بأي حركة من أي نوع في الفراغ، وتختلف جذرياً عن الزخم الزاوي المداري(L). كل الجسيمات الأولية لديها برم خاص بها، فعلى سبيل المثال الإلكترونات لديها (S= 2/1)في حين أن الفوتونات لديها (S= 1)
وقيمة الدوران المحصل تساوي:
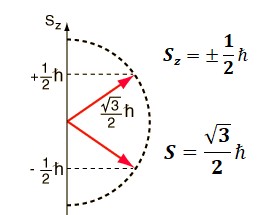
حيث يمثل ħ ثابت بلانك المخفض والذي يساوي :
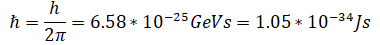
و يمكن التعبير عن العزم المغناطيسي للالكترون من خلال :
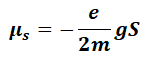
حيث:
e: شحنة الإلكترون
g: معامل لاندي (أو معامل مغناطيسي دوراني في الفيزياء الذرية يعطي مقدار تأثير العزم المغزلي لجسيم (إلكترون) على طاقته بالنسبة لتأثير الزخم الزاوي لمداره عليها ، وذلك عند تواجد الجسيم في مجال مغناطيسي خارجي)
*يتكون الزخم الزاوي الكلي للالكترون(J) من مجموع الزخم الزاوي المداري للالكترون من حركته حول النواة(L) و قيمة الدوران حول نفسه(S) :
J=S+L
حفظ الزخم الزاوي ينطبق على J، ولكن ليس على L ولا S. على سبيل المثال، التفاعل البرمي -المداري يسمح للزخم الزاوي أن ينقل ذهاباً وإياباً ما بين L وS، والمجموع يبقى ثابتاً.
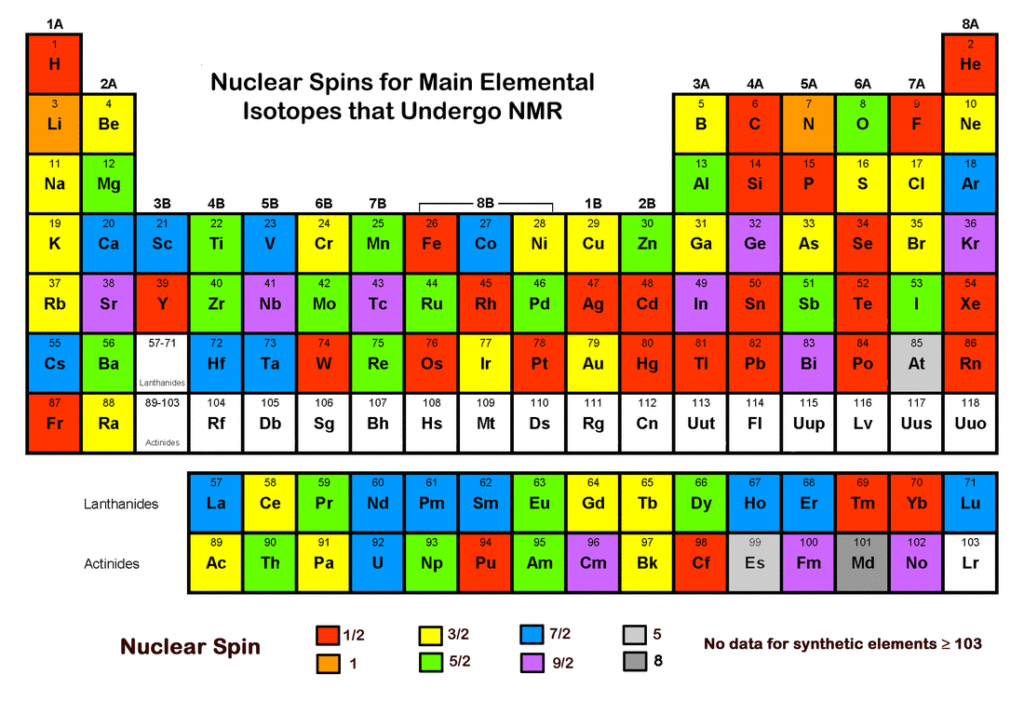
– قيم الدوران النووي(للبروتونات والنيوترونات) تتراوح من( S = 0 )إلى( S = 8 )بزيادة مقدارها ½عبر الجدول الدوري بأكمله. في حين الدوران الإلكتروني له قيمة واحدة فقط (S = ½ ، دائمًا)
-تسمى الجسيمات التي تملك قيمة دوران ممثلة بنصف عدد صحيح مثل البروتونات والإلكترونات الفرميونات( fermions). و تسمى الجسيمات ذات قيمة الدوران الصحيح بوزونات(bosons).
-لم تعد البروتونات والنيوترونات تعتبر جسيمات أولية ، ويتكون كل منها من 3 كواركات متماسكة معًا بواسطة القوة القوية التي تتوسطها الغلونات. الكواركات هي جسيمات أولية لها قيمة دوران تساوي ½(وهذا يفسر وجود زخم للنيوترون). يتكون البروتون من 2 كوارك علوي و1 كوارك سفلي. بشكل عام ، يتم إلغاء اثنين من لفات الكواركات الثلاثة لترك البروتون مع قيمة دوران ½ ، ومع ذلك ، في درجات حرارة عالية جدًا ، قد تدور محاور الكواركات الثلاثة ، مما يمنح البروتون دوران 3/2. يسمى هذا البروتون عالي الطاقة وعالي الدوران جسيم Δ +.
*من اهم التطبيقات على ظاهرة الدوران او العزم المغزلي النووي :
الرنين المغناطيسي النووي (Nuclear magnetic resonance، يرمز له اختصاراً NMR)
تعتمد الطريقة على أن جميع الأنوية الذرية التي فيها عددا فرديا من البروتونات أو النيوترونات يكون لها عزم مغناطيسي ذاتي intrinsic وزخم مداري زاوي. أكثر النوى التي تستخدم في هذه التقنيات هي الهيدروجين-1(S = ½)
-فقط النوى التي تملك قيمة دوران غير صفرية (S ≠ 0) يمكنها امتصاص وإصدار الإشعاع الكهرومغناطيسي وتخضع “للرنين” عند وضعها في مجال مغناطيسي.
-يسمح لنا وجود العزم المغناطيسي للنواة الذرية بمشاهدة اطياف الامتصاص للرنين النووي المغناطيسي حيث أن الرنين يحدث عند انتقال حالة الطاقة بين مستويين للعزم المغزلي في النواة.
-معظم العناصر التي تحتوي فيها النواة على أعداد مزدوجة من البروتونات والنيوترونات يكون لها محصلة عزم مغزلي مساوية للصفر، ولذلك فهي لا تتصرف في وجود مجال مغناطيسي خارجي، بالتالي لا يوجد لتلك العناصر رنين مغناطيسي ومثال على ذلك الأكسجين-18 الذي ليس له رنين نووي مغناطيسي. بينما نجد خاصية الرنين المغناطيسي النووي في نظير عنصر كيميائي مثل الكربون-13 وله رنين نووي مغناطيسي يمكن مشاهدته، وكذلك الفوسفور-31 والكلور-35 ووالكلور-37 كل هذه أنوية لها رنين نووي مغناطيسي.

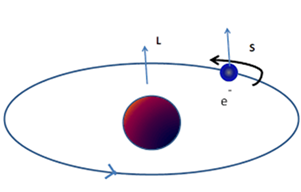
-يمثل الشكل الحركة المتوقعة للالكترون في ذرة الهيدروجين حيث يكون قيمة S =1/2عندما يكون السهم في النصف الاعلى و يكون S=-1/2 عندما يشير الى النصف الاسفل
*وتطبق قياسات اطياف الرنين النووي العالية الدقة على مدى واسع في المجالات الآتية:
-لتحديد المواد الداخلة في التركيبات الكيميائية بدون إفساد المادة
-لتعيين البنية البلورية للجزيئات ( من الجزيئات البسيطة إلى جزيئات البروتين وأجزاء DNA).
-لدراسة تفاعلات الجزيئات مع بعضها البعض.
-بالإضافة إلى الفحوص الطيفية فيمكن بواسطة قياس زمن استرخاء الرنين النووي الحصول على معلومات عن البنية البلورية للمواد وأنظمة حركتها الداخلية.
– فحوص الحركة الانتقالية للجزيئات، مثل تخلل الجزيئات للأغشية أو انتشارها في المحاليل وفي المواد الصلبة
– الفحوص الطبية المتعلقة بالتشخيص التصويري في مجال تشخيص الأورام