ما هو عمر النصف؟
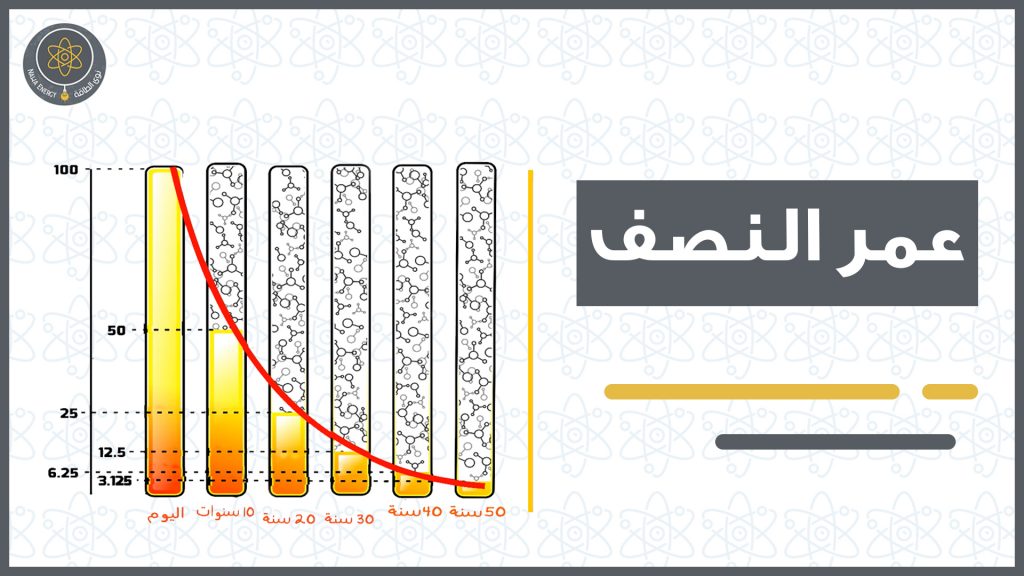
هو الزمن اللازم لنصف كتلة عينة من نظير مشع لتتحلل. يتميّز كُل نظيرٍ مشع بعمر نصف مميز له فقد نجد أن بعض النظائر تتميز بعمر نصف صغير جدًّا يبلغ ثوانٍ أو أقل, ونجد نظائر أخرى على العكس تمامًا لها عمر نصفٍ كبير جدًّا يبلغ آلاف السنين أو ملايين أو حتى مليارات السنين.
يمثل عمر النصف خاصيّة مميزة للمادة مهما كانت كميتها حيث يملك كل عنصر او نظير مشّع عمر نصف خاص به.

| النسبة المئوية المتبقية | الجزء المتبقي | عدد الأعمار النصفية المنقضية |
| 100 | 1⁄1 | 0 |
| 50 | 1⁄2 | 1 |
| 25 | 1⁄4 | 2 |
| 12.5 | 1⁄8 | 3 |
| 6.25 | 1⁄16 | 4 |
في الجدول2 يتبين أنه بعد انقضاء عمر النصف ، أي عند الزمن 1/2 t نجد أن الجزء الباقي من المادة ولم يتحلل قد بلغ النصف . وإذا انتظرنا مدة تالية قدرها 1/2 t نجد أن كمية المادة التي لم تتحلل بعد مقدارها نصف عمر النصف ، أي ربع الكمية الأصلية وهكذا .
ولابد من معرفة ان معادلة التحلل الاشعاعي تتبع التحليل الاسي كما يظهر في الرسم البياني. وأن عمر النصف يختص بالانحلال الاشعاعي وليس الانحلال الذري. وتوضح المعادلة (1) العلاقة بين كمية النويات الأولية N0 في العنصر وكمية النويات عند وقت معين N(t) :
حيث يمثل λ ثابت الانحلال الاشعاعي للعنصر، وكلما قلت كمية عمر النصف زادت كمية ثابت الانحلال الاشعاعي والتالي زادت سرعة انخفاض دالة الاسية e−λt مع الزمن t . والعلاقة بين نصف العمر وثابت الانحلال الاشعاعي هي وفقاً للتالي:
ويمكننا اشتقاق المعادلة (1) من عملية تكامل بسيطة وذلك إذا علمنا أن عدد الانحلالات في فترة زمنية معينة يتناسب مع كمية النويات الأولية :
أو كما اطلقنا سابق على ثابت التناسب وهو ثابت التناسب الاشعاعي وتشير علامة السالب الى تناقص النويات مع كل انحلال:
ومن خلال إعادة ترتيب المعادلة السابقة وباستخدام N(0)= N0 ثم التكامل بفصل المتغيرات سنحصل على المعادلة (1) مرة أخرى:
ولنتمكن من فهم كيف تنقص كمية نويات العنصر إلى النصف في دورة عمر نصف واحدة، لنفترض أن الدورة الأولى تنتهي عند t = t1/2 وباستخدام علاقة عمر النصف وثابت الانحلال الاشعاعي ثم التعويض في المعادلة (1) سنحصل على التالي:
وبناءً على ما سبق وفي حال كانت كمية عمر النصف عدد صحيح فيمكننا فقط قسمة كمية النويات على 2 بدلاً من استخدام المعادلة السابقة، فمثلاً إذا كان هنالك 10 اعمار نصف فيمكننا قسمة عدد النويات الأولية عشرة مرات على 2. أما للأعداد غير الصحيحة من اعمار النصف فيجب استخدام المعادلة (1) للحصول على كمية النويات المتبقية للعنصر.
النشاط الاشعاعي ومعدل الانحلال الاشعاعي:
ما الذي نقصده عندما نقول أن مصدر ما مشع جداً أو عالي الاشعاع؟ بشكل عام نقصد بأن هذا المصدر يقوم بعملية انحلال اشعاعي في زمن معين بكميات كبيرة. لذا فقد اُستخدم مفهوم جديد لقياس هذه الكمية وهو النشاط الاشعاعي R وهو معدل الانحلال الاشعاعي في زمن معين أو وفقاً للصيغة الرياضية التالية:
حيث يمثل ΔN عدد الانحلالات الاشعاعية الحاصل في مدة زمنية تقدر بــ Δt. الوحدة الدولية للنشاط الاشعاعي هي بِيكيريل وتعرف بأنه كمية الانحلال في الثانية الواحدة وتختصر بـ Bq.
1Bq = 1 decay/s
وغالباً يُقاس النشاط الاشعاعي بوحدات أخرى مثل الانحلال في الدقيقة أو في السنة، وهناك وحدة أخرى مشهورة وهي الكوري Ci وهي نشاط جرام واحد من الراديوم-226 أو انحلال 3.70 × 1010 في الثانية. وتعتبر وحدة الكوري وحدة كبيرة بمقارنة بوحدة البِيكيريل:
1MBq = 100 µCi
بديهياً سنعلم أن النشاط الاشعاعي لمصدر مشع سيعتمد على شيئين أثنين: كمية مادة المصدر المشع ومقدار عمر نصف المصدر. فكلما زادت كمية النويات (أي كيمة مادة المصدر المشع)؛ زادت كمية الانحلالات الاشعاعية في زمن معين. وكذلك كلما قل مقدار عمر النصف، زادت كمية الانحلالات الاشعاعية. لذا فإن النشاط الاشعاعي يتناسب تناسباً طردياً مع كمية المادة المشعة الأولية وتناسباً عكسياً مع مقدار عمر النصف. ويمكن صيغة هذا التناسب في العلاقة التالية:
حيث تمثل N كمية المادة المشعة الأولية ويمثل t1/2 عمر نصف المادة. ويمكننا الاستخلاص من المعادلة معادلة للنشاط الاشعاعي وذلك بضرب كلا جهتي المعادلة بـ Δt لنحصل على التالي:
فإذا كان النشاط الاشعاعي R يساوي:
فإن المعادلة النهائية ستكون وفقاً للتالي:
تطبيقات عملية على عمر النصف
لو كان لدينا عنصر التريتيوم وإذا علمت أن فترة عمر النصف لعنصر التريتيوم هي 12.5 سنةً، وكان لدينا 20 جم منهُ ،فكم يتبقى منه بعد 50 سنة؟
المعطيات لدينا هي:
فترة عمر النصف=12.5 سنة
الكتلة في البداية=20 جم
والمطلوب هو:
عدد فترات عمر النصف في 50 سنة
الكتلة المتبقية بعد 50 سنة
لحساب عدد فترات عمر النصف فانها تساوي = المُدة الزمنية/ فترة عمر النصف
وعليه فان عدد فترات عمر النصف للتريتيوم = 12.5/50
أي تساوي 4 فترات .
أما لحساب الكتلة المتبقية فانها تساوي= الكتلة في البداية/2^(عدد فترات عمر النصف)
إذاً الكتلة المتبقية= 4 ^2 /20 =1.25 جم
جهاز قياس الطيف الكتلي(Mass spectrometry)
يستعمل هذا الجهاز في تحديد شكل ونوعية وماهية النظائر والجزيئات وخلائط الكيمياوية والبيولوجية والتي تكون بمقادير صغيرة جدا قد تصل إلى جزء واحد من المليار للغرام الواحد. الجهاز الذي يستعمل هذه الطريقة تم اختراعه في أربعينيات القرن الماضي، ومنذ خمسينيات القرن الماضي يُستعمل هذا الجهاز لتحديد عمر المواد إشعاعيا. يقوم هذا الجهاز بواسطة السخونة الشديدة بشحن مجموعة من الذرات بالأيونات ويتم استخلاص هذه الذرات المتأينة من النموذج ويتم فصل الكتلة والشحنة الكهربائية عن بعضها، عندها يتم قياس الأيونات بواسطة مجسات خاصة تسمى بكؤوس فاراداي – Faraday cup، عندما تتعرض هذه الكؤوس للأيونات هذه فان ذلك يؤدي إلى توليد كهربائية ضعيفة ويتم قياس هذه الكهربائية بدقة وعندها وبواسطة هذه القيم المقاسة يتم معرفة كمية تراكيز العناصر أو النظائر المختلفة (عناصر الأم والبنت).
يمكن أن نرفع دقة قياس العمر بالاشعاع عن طريق أخذ عينات من أماكن مختلفة من النموذج المراد تقدير قِدَمه (عُمْره) لأنه إذا فرضنا أن جميع أجزاء العينة له نفس العمر فيجب منطقيا تعطي كافة القياسات نفس الزمن (العمر) isochron. يمكن مقارنة نتائج فحص نظامين نظائريين مع بعضهما في حالة تواجدهما معا في نفس العينة وذلك للتأكد من دقة القياسات. دقة القياسات تعتمد أيضا على عمر النصف لعنصر الأم. فمثلا نظير كاربون المشع 14C لها عمر نصف أقل من 6000 سنة فليس من المعقول أن نستعمل 14C في تحديد عمر شيء يرجع قِدمه إلى 600 ألف سنة مثلا. لذلك في هذه الحالة يجب استمال أنظمة نظائرية أخرى. أن استعمال نظائر الكربون لتحديد أعمار أشياء ترجع إلى فترة من 1000 سنة إلى 50 ألف سنة قبل الآن يمكن أن يعطي نتائج دقيقة نسبيا.