نقص الكتلة النووية وطاقة الارتباط

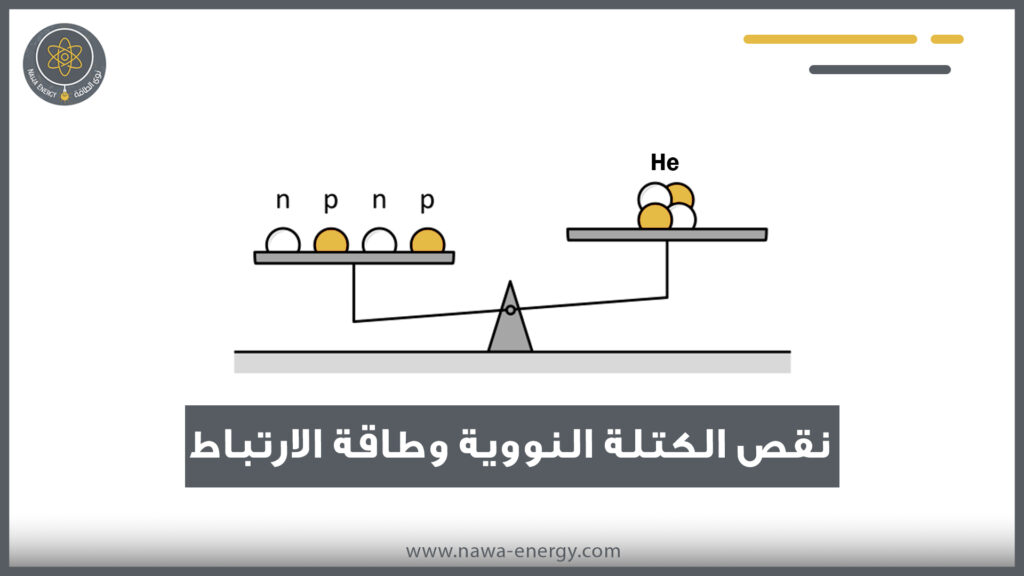
لو أردنا تلخيص مفهوم نقص الكتلة في الفيزياء النووية  (بالإنجليزية : Mass defect) هو الفرق بين مجموع كتل البروتونات والنيوترونات منفردة ومجموع كتلتها مرتبطة ببعضها في داخل النواة الذرية (تكون النواة المتكونة دائمًا أصغر كتلة من مجموع كتل النوكليونات قبل ارتباطها في النواة). وكذلك يكون مجموع كتلة النواة والإلكترونات في ذرة (متعادلة) أكبر من الكتلة الذرية المُقاسة. وهذا الفرق في الكتلة يسمى أيضا نقص الكتلة ولكنه في الذرة يكون أقل بكثير من نقص الكتلة المترتب على ترابط بروتونات مع نيوترونات.

وتنقض هذه الظاهرة قانون حفظ المادة القديم الذي يٌقر بتساوي مجموع الكتل قبل وبعد التفاعل, في حين أن الحقيقة هي نقص الكتلة هنا يتحول إلى طاقة ناتجة عن الالتحام في النواة طبقاً لعلاقة أينشتاين عن تكافؤ المادة والطاقة ، فلا شيء يضيع، وإنما تتغير الكتلة من حال إلى أخر، أي تتحول إلى طاقة.

بالنسبة لنواة ما فإن كل بروتون وكل نيوترون يكون مربوطًا داخل النواة بنفس طاقة الربط وهي (E₀), تختلف قيمة E₀ من عنصر لآخر كما هو مبين في (الشكل 2) الذي يمثل منحنى الاستقرار الرابط بين العدد الكتلي (A) ومعدل طاقة الربط النوويّة E₀ . وخلافًا لطاقة ربط الإلكترونات الذرية التي لا تتجاوز بضع وحدات من الإلكترون فولت فإن النيوكليونات ترتبط داخل النواة بطاقات أكبر من ذلك بملايين المرات كما يظهر في الشكل. تصل E₀ إلى قيمتها العظمى للعناصر المحيطة بالحديد (A = 26) وتكون أصغر من ذلك بالنسبة للنوى التي قيم عددها الذري أكبر من ذلك أو أصغر. وهذا يقدم مؤشرًا على الاستقرار النووي.

و من الممكن أن نستخدم مصطلح طاقة الوضع النووية :هي الطاقة المخزنة في الروابط النووية و حين تكسر هذه الروابط يتم تدمير الكتلة و تنشأ الطاقة الحركية الحرارية .و هي الطاقة الكامنة للجسيمات مثل البروتونات والنيوترونات الموجودة داخل نواة الذرة. فعليًا طاقة الارتباط للنويدات هي نفس الطاقة التي نحتاجها لتكوين النواة .

المعادلة المستخدمة لحساب طاقة الوضع النووي و الطاقة الناتجة عن نقص الكتلة هي معادلة اينشتان الشهيرة :

حيث m تمثل كتلة الجسم و c سرعة الضوء في الفراغ و تساوي:

أمثلة على ذلك:

• ما يحدث في المفاعل النووي
• ما يحدث في القنبلة الذرية 
• ما يحدث في الشمس والنجوم

تكون الروابط النووية موجودة بين الجسيمات كالاتي:

• (p-p) بين بروتونين 
• (n-n) بين نيوترونين
• (n-p) بين نيوترون وبروتون

يوجد ثلاث طرق لكسر هذه الروابط و إطلاق الطاقة النووية :

• الإنشطار
• الإندماج 
• تفاعل الإبادة: المادة مع المادة المضادة

نحن نعلم أنه بالإمكان معرفة كتلة أي شيء إذا عرفنا كتلة مكوناته ولكن لنفترض الآن أن لدينا نواة وقمنا بتفكيكها، لتتم عملية تفكيك هذه النواة يجب علينا أن نضيف طاقة إلى النواة لنتغلب على القوة النووية القوية التي تُبقي النواة متماسكة، هذه الطاقة المضافة  تساوي طاقة الربط النووية. وإذا افترضنا أن مكونات النواة وهم البروتونات والنيوترونات كانوا بوضع السكون عندما فككناهم، فإن الطاقة المضافة إلى النواة تحولت إلى كتل سكونية للبروتونات  والنيوترونات مما يعني أن كتلهم زادت مقارنةً بكتلتهم وهم مجتمعين في النواة، فالفرق بين الكتل السكونية قبل وبعد التفكيك هو النقصان الكتلي Δm والذي يساوي:

Δm = BE/c²

 فإذا كانت نواة ^AX  لديها عدد Z من البروتونات وعدد N من النيوترونات، عندها يكون النقصان الكتلي Δm يساوي:

Δm = (Zm_p + Nm_n) − m_t

حيث أن m_t   هي كتلة النواة ^AX, وكتلة البروتونات هي Zm_p   في حين أن Nm_n  هي كتلة النيوترونات

وعند التعويض في معادلة تكافؤ الكتلة مع الطاقة نجد أن طاقة الربط النووية BE تساوي:

BE = (∆m)c² = [(Zm_p + Nm_n) − m_t]c²

وكوننا لا نتعامل مع كتل نويات العناصر، فالجدول الدوري يعطينا كتل الذرات أي كتلة النواة مع إلكتروناتها. لهذا من المناسب تحويل المعادلة السابقة إلى معادلة كتل ذرية بدل من الكتل النووية حيث أن كتلة الذرةm(^AX)   تساوي:

m(^AX)=  m_t+ Zm_e

أو 

m_t= m(^AX)  − Zm_e

حيث أن Z هو عدد إلكترونات الذرة أما m_e  فهي كتلة الإلكترون وبالتعويض في المعادلة نحصل على:

BE = (∆m)c² = [(Zm_p + Nm_n) – (m(^AX)  − Zm_e) ]c²

وبإعادة ترتيب المعادلة السابقة نحصل على:

BE = (∆m)c² = [(Zm_p + Nm_n+ Zm_e) – m(^AX)]c²

أو

BE = (∆m)c² = [(Z(m_p+m_e)+ Nm_n) – m(^AX]c²

وإذا علمنا أن  (m_p +m_e) ما هي إلا كتلة ذرة الهيدروجين  m(¹H)كونها تتكون من إلكترون واحد وبرتون واحد، وبذلك تصبح المعادلة:

BE = {[Zm(¹H) + Nm_n] − m(^AX)}c²

دعونا نطبق هذا مع نواة الهيليوم  ⁴He فلو جئنا لمكونات الهيليوم لعرفنا أنها عبارة عن نيوترونان وبروتونان

وبما أن كتلة البروتون الواحد = 1.00727647 وحدة كتل ذرية (Amu)
وكتلة النيوترون الواحد =1.00866490 وحدة كتل ذرية (Amu)
فمن المفترض أن كتلة نواة الهيليوم تحسب كالتالي:

2*كتلة البروتون +2*كتلة النيوترون
أي
(2*1.0072647)+(2*1.00866490)     

والذي يعطينا الكتلة المتوقعة والتي تساوي =4.0318592 amu
ولكنّ الكتلة الحقيقة لنواة الهيليوم تساوي=4.00150608 amu
أي أنها أقل من الكتلة المتوقعة فأين ذهب هذا الفرق في الكتلة الذي يساوي 0.03035312 amu
إن هذا الفرق يسمى نقص الكتلة وقد تحول إلى طاقة يمكن حسابها من خلال معادلة أينشتاين التي تحسب الطاقة الناتجة عن تحول الكتلة إلى طاقة:

وفي نواة الهيليوم بعد تحويل فرق الكتلة إلى وحدة الغرام لو طبقنا في المعادلة سنجد أن مقدار هذه الطاقة يساوي 
4.53346* 10^-12 جول. وهذه هي الطاقة التي انبعثت عند تكون أو تشكل النواة وهذا الانبعاث من الطاقة هو الذي يُبقي النواة مستقرة ومترابطة وتسمى هذه الطاقة طاقة الربط النووية, ومن جهة أخرى لو أردنا تفكيك النواة علينا تزويد النواة بنفس هذا المقدار من الطاقة الذي جعلها مترابطة.